
Contents
Components of a Business Information System
Two Theoretical Relational Languages
This text on SQL is based on the Oracle Database using the EP-European Parliament as Data Model.
The European Parliament (EP) is the parliamentary institution of the European Union (EU).
The European Parliament is elected by the citizens of the European Union to represent their interests.
Its origins go back to the 1950s and the founding Treaties. Since 1979 its members have been directly elected by the citizens of the EU.
Elections are held every five years, and every EU citizen is entitled to vote, and to stand as a candidate, wherever they live in the EU. Parliament thus expresses the democratic will of the European Union's nearly 500 million citizens and it represents their interests in discussions with the other EU institutions.
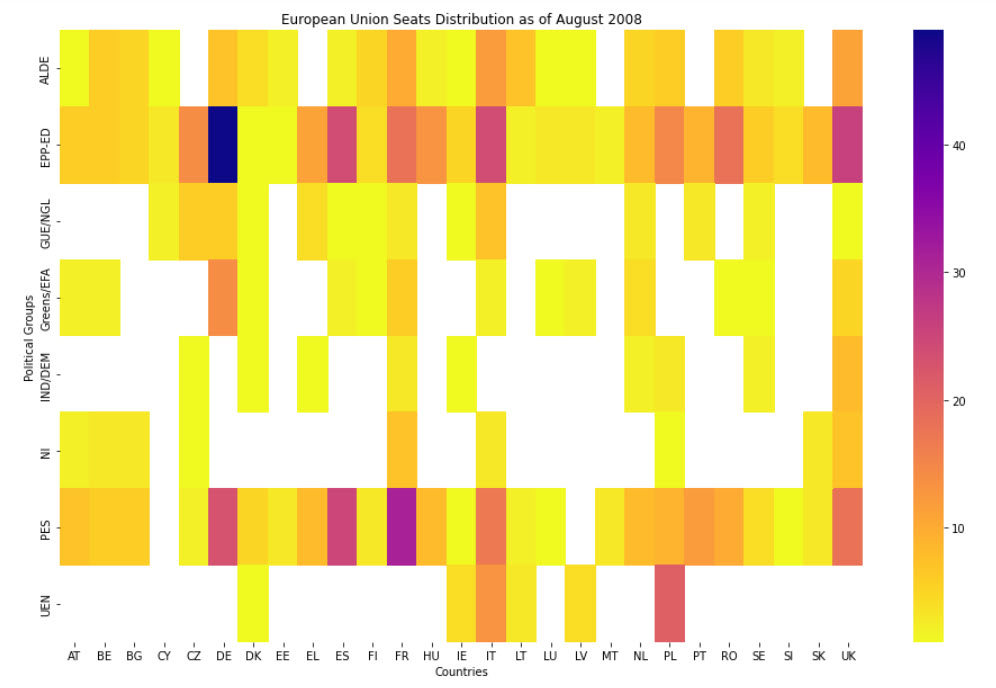
The European Parliament model and data used in this SQL text, are based on the elections which were held in June 2004. The European Parliament of 2004 elections had 785 members from all 27 EU countries.
The sources for the data, which are all freely obtainable from the European Union website, and from several leaflets of the EU institutions, are listed in the References section.
These sources are used to create the fictitious Business Narrative of the "Data Modelling and Normalization" Chapter.
We called this Business Narrative; "the Story of the European Union" which explains about the EU and EP, for purposes of Data Modeling.
The Story of the European Union is the last Chapter of Kaye is Learning SQL.


A Business Information System Consists of the Following Components:





Users are personnel who use the system.
They can be
Or, they can be
In short, anybody who is responsible of doing at least one piece of work in their workplace ...
We simply call all of them

A report which is one of the application programs in a Business Information System, helps users take their business decisions.
Sometimes, these decisions have to be made immediately – they can be daily decisions, hourly decisions or even minutely decisions.
Sometimes decisions have to be made whose results will affect a business in the long run.
These reports are also known as the "Business Intelligence" of a company.
Whether they will affect this very minute, or a ten years’ span, the users need the "information" in these reports..
Information that is necessary to take the right decisions – the decisions that are vital for a business to operate and to be successful.
Information itself uses "data" stored in the Database and managed by the Database Management System Software .
And when the data are processed – that is when they are manipulated, collected and organized, the result is information.
Below are some of the basic terms used, to describe the building blocks of a database.
An Entity can be;
An Entity is a thing of significance about which information needs to be known.
Example
If you were a statistician in EUROSTAT-the statistical office of the European Commission, you would like to have all the information about the European Union member countries.
A COUNTRY is an Entity Type or an Entity Class.
However, each COUNTRY in the European Union is an Entity Instance .
For example, Belgium and Poland are Entity Instances of the Entity Type COUNTRY.
There is only one Entity Type/Class of COUNTRY, whereas there are twenty-seven Instances of this entity.
Another Example
If you were working in the DG(Directorate-General) Personnel of the European Parliament , you would like to have all the information about the Members of the European Parliament(MEPs).
A MEMBER OF THE PARLIAMENT is an Entity Type or an Entity Class, and each Member of the Parliament is an Entity Instance.
There is only one Entity Type/Class of MEMBER OF THE PARLIAMENT, whereas there are 785 Instances of this entity.
An attribute is a characteristic that describes an entity.
Example
Some of the likely "attributes" for a country are;
Another Example
Some of the likely "attributes" for an MEP are;
Reationships are interactions between Entities.
They are described by "verbs".
Example
A Member of the European Parliament(MEP) belongs to a Political Group.
Therefore, we can say that the Relationship between the Entity MEP and the Entity POLITICAL GROUP is "belongs to".
Now that we know briefly about the concepts of "Entity" and "Relationship", we can say that;
a Database is made up of a Collection of Entities and the Relationships between these Entities.
Example
European Parliament's database may be made up of a Collection of the Entities "COUNTRY", "POLITICAL GROUP", "MEMBER OF THE PARLIAMENT", "DELEGATION", "ROLE" and the Relationships between these Entities.
When we design a database, we need to create Entities each of which is a collection of entity instances. For example Entity POLITICAL GROUP and the Entity MEP (Members of the European Parliament).
When we design a database, we also have to establish the "relationships" between these "entities".
Depending on the type of interaction, the relationships are classified into three categories:
How to Determine the Relationship Type
A one-to-one relationship is written as 1:1 in short form.
Entities X and Y have a 1:1 relationship if the following conditions hold:
Let's say in our database, there is an Entity called COUNTRY, and an Entity called CAPITAL.
Entity COUNTRY contains all the countries in the world.
Each country in the world is an instance of this Entity.
Entity CAPITAL contains all the capitals in the world.
Each capital in the world is an instance of this Entity.
The RELATIONSHIP between these two entities is:
A COUNTRY has one and only one CAPITAL, and a CAPITAL belongs to one and only one COUNTRY.
We say that, the entities COUNTRY and CAPITAL have a 1:1 relationship.
A one-to-many relationship is written as 1:M in short form.
Entities X and Y have a 1:M relationship if the following conditions hold:
Let's say in our database, there is an Entity called POLITICAL GROUP, and an Entity called MEMBER OF THE PARLIAMENT.
The Entity POLITICAL GROUP contains all the political groups in the European Parliament.
Each political group in the European Union is an instance of this Entity.
The Entity MEMBER OF THE PARLIAMENT contains all the Members of the European Parliament(MEPs).
Each MEP is an instance of this Entity.
The RELATIONSHIP between these two entities is:
A POLITICAL GROUP in the European Parliament has many MEMBERs OF THE PARLIAMENT, but a MEMBER OF THE PARLIAMENT belongs to one and only one POLITICAL GROUP.
We say that, the entities POLITICAL GROUP and MEMBER OF THE PARLIAMENT have a 1:M relationship.
A many-to-many relationship is written as M:M or M:N in short form.
Entities X and Y have a M:M relationship if the following conditions hold:
Let's say in our database, there is also an entity called ROLE.
We already know that there is an Entity called MEMBER OF THE PARLIAMENT in our database.
The entity ROLE contains all the roles held by the MEPs, that is all the roles held by the Members of the European Parliament.
Each Role held by an MEP is an instance of this entity.
The Entity MEMBER OF THE PARLIAMENT contains all the Members of the European Parliament (MEPs).
Each MEP is an instance of this Entity.
Each MEP in the European Parliament has at least one Role.
The RELATIONSHIP between these two entities is:
A MEMBER OF THE PARLIAMENT may have many ROLEs, and a ROLE may be held by more than one (by many) MEMBERs OF THE PARLIAMENT.
We say that the entities MEMBER OF THE PARLIAMENT and ROLE have a M:M relationship.
To determine the Type of Relationship between the Entity X and the Entity Y, we can ask the following two questions:

Depending on the answers to these two questions, we can determine the type of relationship, between the two entities.
How this is achieved, is illustrated below:

If a Database Management System is based on a Relational Database Model, then it is also known as a Relational Database Management System - an RDBMS.
In this course, we base our learnings on the Relational Database Model.
E.F.Codd (Edgar F. "Ted" Codd) developed the "relational database model" in 1970.
This new concept is published in the Communications of the Association for Computing Machinary (CACM), in his article named "A Relational Model of Data for Large Shared Data Banks".
The model is based on Mathematical Set Theory.
It uses "relation" as the building block of the database.
The relation is represented by a two-dimensional, flat structure also known as a "table".
The user views the data in a logical, two-dimensional structure.
A table is a matrix of rows and columns in which;
We refer to a Relation as an Entity at the Data Modeling and Database Design stage.
When the physical database is created, Entities become Tables.
We will use the following concepts interchangeably for the rest of this chapter:
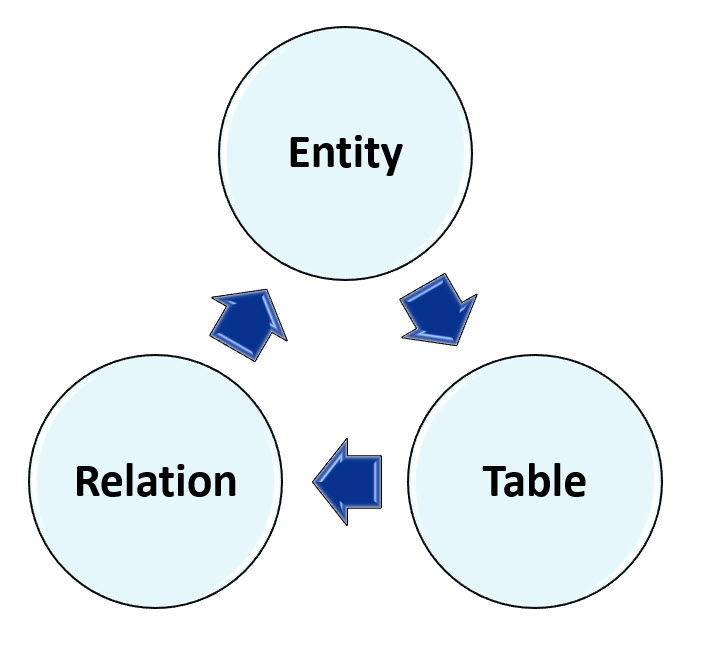
We refer to a Relation as an Entity at the Data Modeling and Database Design stage.
When the physical database is created, Entities become Tables.
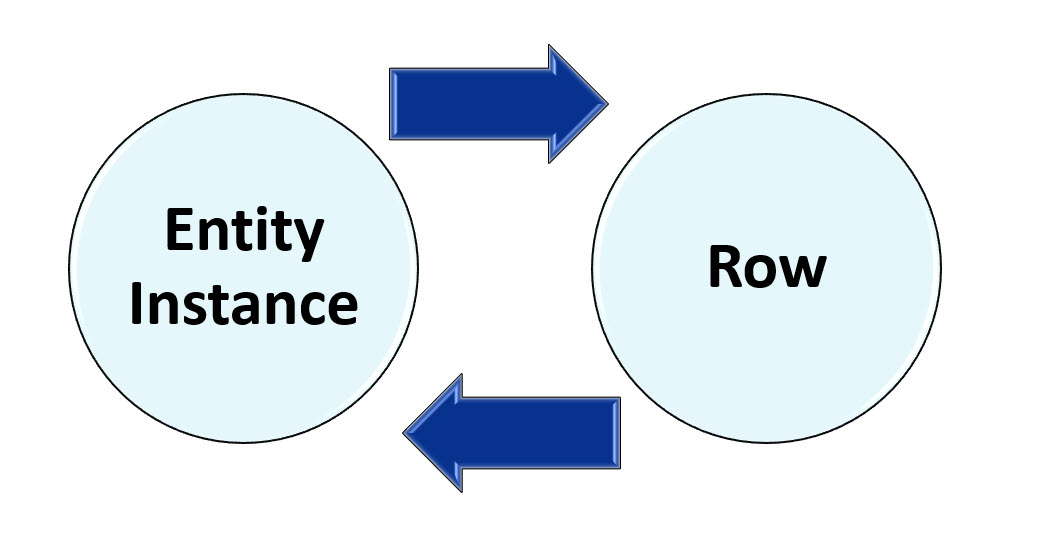
A table is a matrix of rows and columns in which;
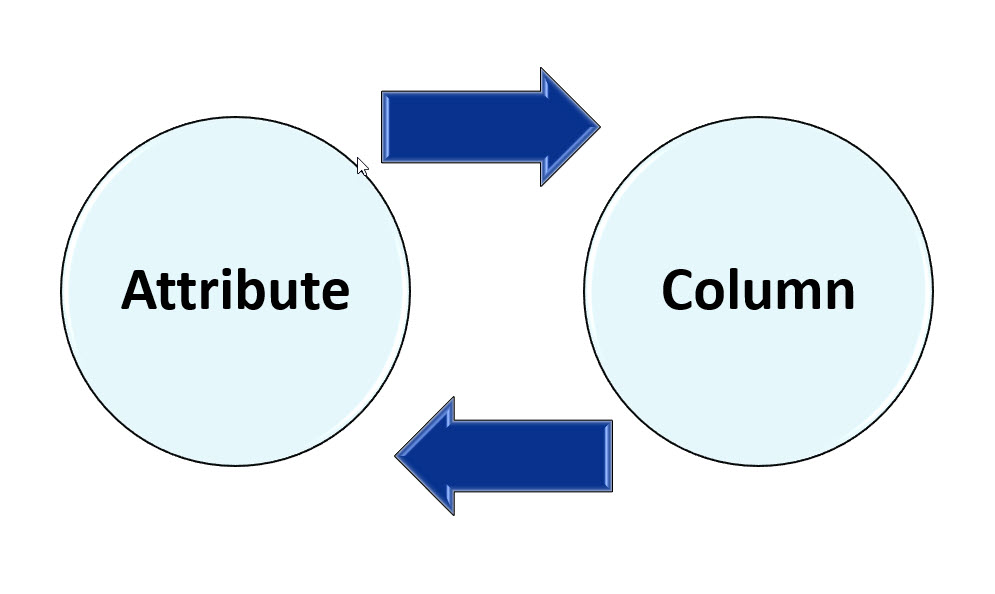
A table is a matrix of rows and columns in which;
We will use the following Relations-Entities-Tables of a Sample European Research Institution to learn new terminology:
| Relation-Entity-Table | Definition |
|---|---|
| PROJECTS | Holds details of research projects. A research project may span a period of several years. |
| PROGRAM_PROJECTS | Holds details of programs. A program can contain several numbers of different projects. |
| PROGRAMS_LAST_YEAR | Contains details of programs that consist of research projects, their countries and locations, which started last year. |
| PROGRAMS_THIS_YEAR | Contains details of programs that consist of research projects, their countries and locations, which started this year. |
| STAFF | Holds details of staff responsible of each project and their department number. |
| DEPARTMENTS | Holds details of departments. |
| project no | project type | description | main sponsor | cost (million Euros) |
|---|---|---|---|---|
| 100 | ATOMS | Nano Technology | Futuristic | 2.37 |
| 200 | BITS | Information Technology | Guru | 6.19 |
| 300 | GENES | Bio Technology | Longevity | 4.48 |
| 400 | NEURONS | Neuro Science | Cyberlabs | 1.49 |
PROJECTS has;
| program no | project no | number of projects |
|---|---|---|
| 10 | 100 | 2 |
| 10 | 200 | 4 |
| 20 | 100 | 1 |
| 20 | 300 | 1 |
| 30 | 100 | 2 |
| 30 | 200 | 2 |
| 30 | 300 | 4 |
| 30 | 400 | 3 |
| 40 | 100 | 2 |
| 60 | 100 | 1 |
PROGRAM_PROJECTS has;
| program no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 20 | Brussels | Belgium |
| 30 | Luxembourg | Luxembourg |
PROGRAMS_LAST_YEAR has;
| program no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 30 | Luxembourg | Luxembourg |
| 40 | Warsaw | Poland |
| 60 | Prague | Czech Republic |
PROGRAMS_THIS_YEAR has;
| staff id | name | dg id | program_no |
|---|---|---|---|
| 802 | YILDIZ | 400 | 10 |
| 804 | HEYNEN | 400 | 20 |
| 806 | KANUITH | 400 | 30 |
| 808 | ZABOROWSKI | 400 | 40 |
| 1020 | OTTOVA | 400 | 60 |
STAFF has;
| dg id | dg name |
|---|---|
| 200 | DG Communications |
| 400 | DG Innovation and Research |
| 600 | DG Legal Service |
DEPARTMENTS has;
In relational terminology, a Row in a Table or an Instance of an Entity is referred to as a Tuple.
The number of columns in a table is called the Degree of the relation.
For instance, if a table has four columns, then the table is of degree 4.
Just like the order of rows is not important in a Relational Database Model, the order of the columns is not important either.
The set of all possible values that a column may have is called the Domain of that column.
An Example for Domain
The domain of the "dg_name" column of the "DEPARTMENTS" table is the set of all possible Directorate-Generals in this Research Institution.
This domain can be;
Another Example for Domain
Domain of the "country" column of the PROGRAMS_THIS_YEAR table, is the set of all countries that take part in the European Research Project, namely, all the EU Member and Candidate countries;
In our tables, the columns;
all have numeric values, but their use is different. Therefore they do not have the same domain.
Two domains are the same only if they have the same values and the same use.
A Key is a minimal set of columns used to uniquely identify each row in a table.
If a single column can be used to identify each row, there is no need to use two columns as a key.
An Example for a Single Column Key
In PROGRAMS_LAST_YEAR and PROGRAMS_THIS_YEAR, "program_no" column uniquely identifies each row.
| program no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 20 | Brussels | Belgium |
| 30 | Luxembourg | Luxembourg |
| program no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 30 | Luxembourg | Luxembourg |
| 40 | Warsaw | Poland |
| 60 | Prague | Czech Republic |
In these tables, the column "program_no" is a Single Column Key.
Another Example for a Single Column Key
In PROJECTS, "project_no" column uniquely identifies each row.
| project no | project type | description | main sponsor | cost (million Euros) |
|---|---|---|---|---|
| 100 | ATOMS | Nano Technology | Futuristic | 2.37 |
| 200 | BITS | Information Technology | Guru | 6.19 |
| 300 | GENES | Bio Technology | Longevity | 4.48 |
| 400 | NEURONS | Neuro Science | Cyberlabs | 1.49 |
In PROJECTS, the column "project_no" is a Single Column Key.
Example for a Key with More Than One Column
In PROGRAM_PROJECTS, none of the columns can uniquely identify a row.
In this table, a combination of columns must be used to uniquely identify a row.
This combination is "program_no" and "project_no" cloumns.
| program no | project no | number of projects |
|---|---|---|
| 10 | 100 | 2 |
| 10 | 200 | 4 |
| 20 | 100 | 1 |
| 20 | 300 | 1 |
| 30 | 100 | 2 |
| 30 | 200 | 2 |
| 30 | 300 | 4 |
| 30 | 400 | 3 |
| 40 | 100 | 2 |
| 60 | 100 | 1 |
In the PROGRAM_PROJECTS table, "program_no" and "project_no" columns together can be used as a key, to uniquely identify each row.
UNIQUE IDENTIFIER
A KEY Column, or a Combination of Columns that act as a KEY , is sometimes called a UNIQUE IDENTIFIER.
When a Single Column is used as a Unique Identifier , then this column is known as the Primary Key of the table.
For example, "project_no" column is the Primary Key of the PROJECTS table.
When a Combination of Columns is used as a Unique Identifier, then these columns are known as;
Sometimes a more human approach is used to identify or retrieve a row from a table.
This is because, it is not possible to remember primary key values such as;

In such cases,
Such a key is known as a Secondary Key.

If none of the columns in a table is a candidate for the primary key, then database designers can use an extra column as the primary key.
In some cases, this can be preferred to having a composite primary key.
Such a key, which is a Unique Identifier for the row it belongs to, is known as a Surrogate Key.
One way of generating column values for the Surrogate Key Columns in Oracle is, to use the Sequence object.
In a relational database, tables are related to each other through a common column.
A column in a table that references a column in another table is known as a Foreign Key.
For example, the "project_no" column is a Foreign Key column in the PROGRAM_PROJECTS table, that References the "project_no" column in the PROJECTS table.
| program no | project no | number of projects |
|---|---|---|
| 10 | 100 | 2 |
| 10 | 200 | 4 |
| 20 | 100 | 1 |
| 20 | 300 | 1 |
| 30 | 100 | 2 |
| 30 | 200 | 2 |
| 30 | 300 | 4 |
| 30 | 400 | 3 |
| 40 | 100 | 2 |
| 60 | 100 | 1 |
| project no | project type | description | main sponsor | cost (million Euros) |
|---|---|---|---|---|
| 100 | ATOMS | Nano Technology | Futuristic | 2.37 |
| 200 | BITS | Information Technology | Guru | 6.19 |
| 300 | GENES | Bio Technology | Longevity | 4.48 |
| 400 | NEURONS | Neuro Science | Cyberlabs | 1.49 |
Although we will learn about the concepts of integrity later in this SQL Course in detail, here is an early introduction.
In a database managed by a Relational Database Management System, it is very important that the data in the underlying tables are kept consistent.
If consistency is compromised, then data become unusable.
Integrity Rule #1 Entity Integrity
Integrity Rule #2 Referential Integrity
This fact led to the following two Integrity Rules:

Integrity Rule #1 Entity Integrity
Integrity Rule #1 Entity Integrity
NULL
Integrity Rule #1 Entity Integrity
If the Primary Key value in a row is Null, then we do not have enough information about the row to uniquely identify it.
Integrity Rule #1 Entity Integrity
Integrity Rule #1 Entity Integrity
Please note that the Designers, DBAs and Developers of a Database Design Team MUST define the Primary Key for the RDBMS Software to follow this rule.
Integrity Rule #2 Referential Integrity
For example, the "project_no" column is a Foreign Key column in the PROGRAM_PROJECTS table, that References the "project_no" column which is the Primary Key of the PROJECTS table.
| program no | project no | number of projects |
|---|---|---|
| 10 | 100 | 2 |
| 10 | 200 | 4 |
| 20 | 100 | 1 |
| 20 | 300 | 1 |
| 30 | 100 | 2 |
| 30 | 200 | 2 |
| 30 | 300 | 4 |
| 30 | 400 | 3 |
| 40 | 100 | 2 |
| 60 | 100 | 1 |
| project no | project type | description | main sponsor | cost (million Euros) |
|---|---|---|---|---|
| 100 | ATOMS | Nano Technology | Futuristic | 2.37 |
| 200 | BITS | Information Technology | Guru | 6.19 |
| 300 | GENES | Bio Technology | Longevity | 4.48 |
| 400 | NEURONS | Neuro Science | Cyberlabs | 1.49 |
Integrity Rule #2 Referential Integrity
If a user and/or an application program enters a value in the Foreign Key column of a Table, Oracle cross-references the Referenced Table's Primary Key column to confirm the existence of such a value.
Integrity Rule #2 Referential Integrity
Please note that the Designers, DBAs and Developers of a Database Design Team MUST define the Foreign Key and the Primary Key it references, for the RDBMS Software to follow this rule.
E.F. Codd suggested Two Theoretical Relational Languages to use with the Relational Model:
In the database systems available today, nonprocedural Structured Query Language SQL is used as a data-manipulation language.
The two theoretical languages which will be explained below, have provided the basis for SQL.
Relational algebra is a procedural language.
It is the manipulative part of Relational Model as suggested by E.F. Codd.
"Relational Algebra is basically a Set of Operators that take Relations as their operands and return a Relation as their result."
The nine Operations used by Relational Algebra are as follows:
Applications of Relational Algebra
Weaknesses of Relational Algebra as a Programming Language
Strengths of Relational Algebra as a Programming Language
The UNION of two tables results in retrieval of all rows that are in one or both tables.
The duplicate rows are eliminated from the resulting table -- the resulting table does not contain two rows with identical data values.
Union Compatiblility

Two tables that satisfy the requirements above are said to be Union Compatible.
If we want to see all the programs that took place last year and programs taking place this year, we can perform a UNION on the PROGRAMS_LAST_YEAR and PROGRAMS_THIS_YEAR tables.
If we call the resulting table TABLE_A, the operation can be denoted by:
| program_no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 20 | Brussels | Belgium |
| 30 | Luxembourg | Luxembourg |
| program_no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 30 | Luxembourg | Luxembourg |
| 40 | Warsaw | Poland |
| 60 | Prague | Czech Republic |
| program_no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 20 | Brussels | Belgium |
| 30 | Luxembourg | Luxembourg |
| 40 | Warsaw | Poland |
| 60 | Prague | Czech Republic |
If we want to find out the programs that took place BOTH LAST YEAR and CONTINUING THIS YEAR, we can perform an INTERSECTION operation on the PROGRAMS_LAST_YEAR and PROGRAMS_THIS_YEAR tables.
If we call the resulting table of this INTERSECTION OPERATION, TABLE_B, then the operation can be denoted by:
| program_no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 20 | Brussels | Belgium |
| 30 | Luxembourg | Luxembourg |
| program_no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 30 | Luxembourg | Luxembourg |
| 40 | Warsaw | Poland |
| 60 | Prague | Czech Republic |
TABLE_B = PROGRAMS_LAST_YEAR INTERSECTION PROGRAMS_THIS_YEAR
| program_no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 30 | Luxembourg | Luxembourg |
The resulting table TABLE_B shows us those programs which started last year or before and continuing this year.
If we want to find out the programs which took place LAST YEAR, BUT DO NOT CONTINUE THIS YEAR, we can perform a DIFFERENCE operation on the PROGRAMS_LAST_YEAR and PROGRAMS_THIS_YEAR tables.
If we call the resulting table of this DIFFERENCE OPERATION, TABLE_C, then the operation can be denoted by:
| program_no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 20 | Brussels | Belgium |
| 30 | Luxembourg | Luxembourg |
| program_no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 30 | Luxembourg | Luxembourg |
| 40 | Warsaw | Poland |
| 60 | Prague | Czech Republic |
| program_no | location | country |
|---|---|---|
| 20 | Brussels | Belgium |
The resulting table TABLE_C shows us those programs which took place last year and do not continue this year.
Just as in Mathematics, in Relational Algebra also, A - B may not be equal to B - A.
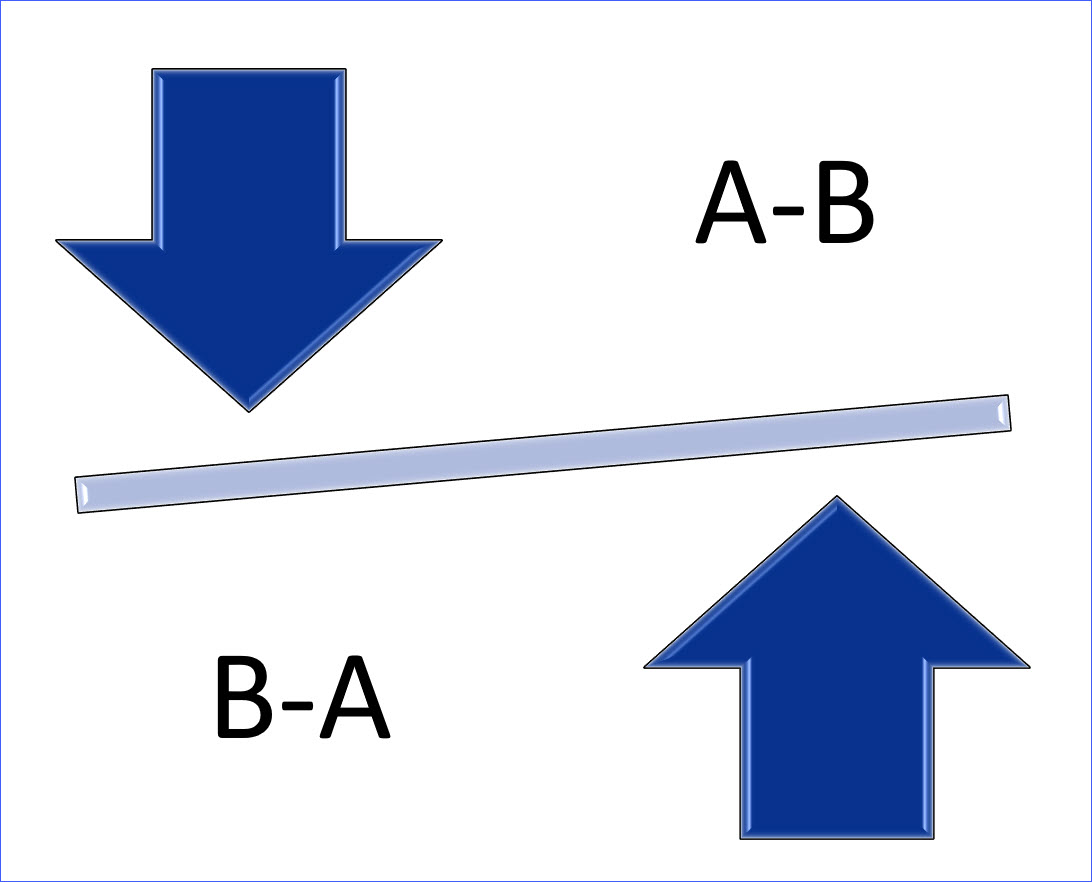
If we want to find out those programs which DID NOT EXIST LAST YEAR, BUT STARTED THIS YEAR, we can perform a DIFFERENCE operation on the PROGRAMS_THIS_YEAR and PROGRAMS_LAST_YEAR tables.
If we call the resulting table of this DIFFERENCE OPERATION, TABLE_D, then the operation can be denoted by:
| program_no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 30 | Luxembourg | Luxembourg |
| 40 | Warsaw | Poland |
| 60 | Prague | Czech Republic |
| program_no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 20 | Brussels | Belgium |
| 30 | Luxembourg | Luxembourg |
| program_no | location | country |
|---|---|---|
| 40 | Warsaw | Poland |
| 60 | Prague | Czech Republic |
The resulting table TABLE_D shows us those programs which started this year.
The PROJECTION Operation returns VERTICAL SLICES from a table.
For example, we might like to list only the DESCRIPTION and the MAIN_SPONSOR columns of the PROJECTS table.
| project no | project type | description | main sponsor | cost (million Euros) |
|---|---|---|---|---|
| 100 | ATOMS | Nano Technology | Futuristic | 2.37 |
| 200 | BITS | Information Technology | Guru | 6.19 |
| 300 | GENES | Bio Technology | Longevity | 4.48 |
| 400 | NEURONS | Neuro Science | Cyberlabs | 1.49 |
PROJECTION Operation is indicated by;
If we call the Resulting Table of this PROJECTION Operation, TABLE_E, then the operation can be denoted by:
| description | main sponsor |
|---|---|
| Nano Technology | Futuristic |
| Information Technology | Guru |
| Bio Technology | Longevity |
| Neuro Science | Cyberlabs |
The SELECTION Operation returns HORIZONTAL SLICES from a table.
For example, we might like to list only "those projects which cost more than 3 million Euros" in the PROJECTS table.
| project no | project type | description | main sponsor | cost (million Euros) |
|---|---|---|---|---|
| 100 | ATOMS | Nano Technology | Futuristic | 2.37 |
| 200 | BITS | Information Technology | Guru | 6.19 |
| 300 | GENES | Bio Technology | Longevity | 4.48 |
| 400 | NEURONS | Neuro Science | Cyberlabs | 1.49 |
SELECTION Operation is indicated by;
If we call the Resulting Table of this SELECTION Operation, TABLE_F, then the operation can be denoted by:
| project no | project type | description | main sponsor | cost (million Euros) |
|---|---|---|---|---|
| 200 | BITS | Information Technology | Guru | 6.19 |
| 300 | GENES | Bio Technology | Longevity | 4.48 |
For simplicity we take two tables with one column each and perform the PRODUCT Operation on them.
| T1_COLUMN1 |
|---|
| A |
| B |
| C |
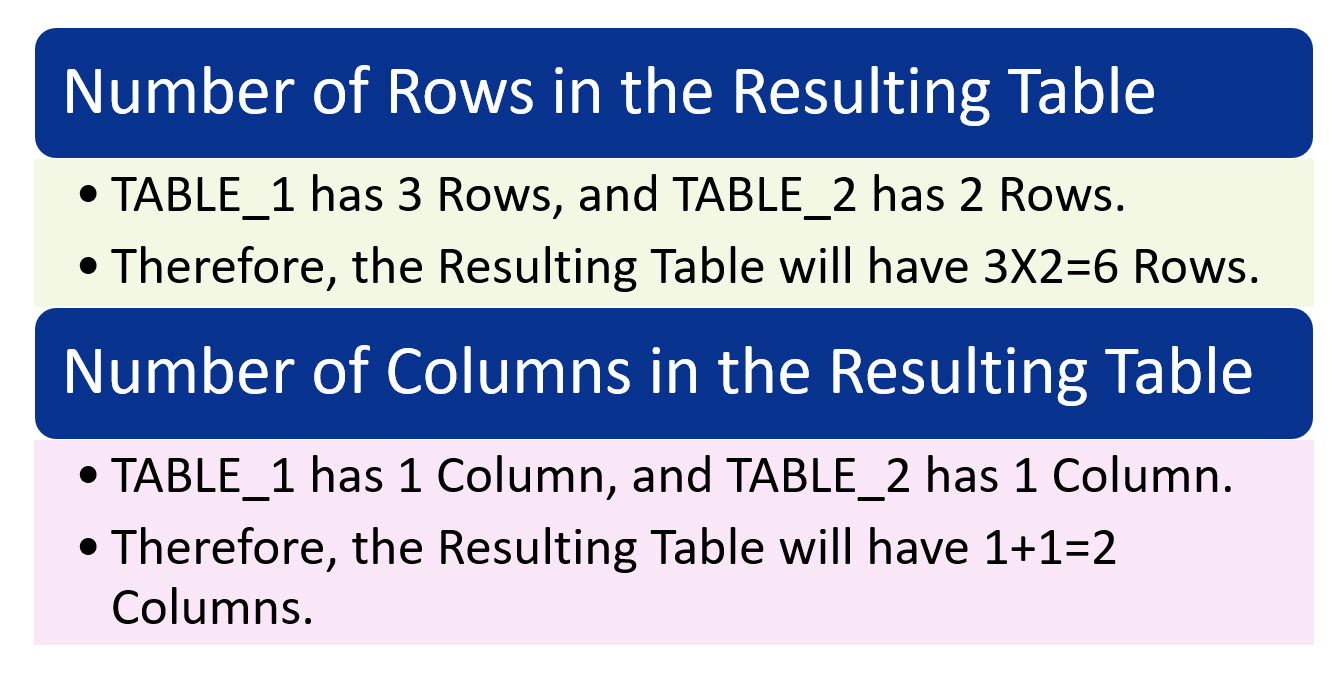
TABLE_1 has 1 Column and 3 Rows.
| T2_COLUMN1 |
|---|
| 10 |
| 20 |
TABLE_2 has 1 Column and 2 Rows.
What will the Result of the PRODUCT Operation be?
If we call the Resulting Table of this PRODUCT Operation, TABLE_G, then the operation can be denoted by:
| T1_COLUMN1 | T2_COLUMN1 |
|---|---|
| A | 10 |
| A | 20 |
| B | 10 |
| B | 20 |
| C | 10 |
| C | 20 |
The Resulting Table of the PRODUCT Operation on TABLE_1 and TABLE_2, which is TABLE_G, has 6 Rows and 2 Columns.
Another Example on the PRODUCT Operation
Now, let us take the STAFF and the DEPARTMENTS tables, and perform the PRODUCT operation on these two tables.
STAFF table has 5 rows and 4 columns:
| staff id | name | dg id | program no |
|---|---|---|---|
| 802 | YILDIZ | 400 | 10 |
| 804 | HEYNEN | 400 | 20 |
| 806 | KANUITH | 400 | 30 |
| 808 | ZABOROWSKI | 400 | 40 |
| 1020 | OTTOVA | 400 | 60 |
DEPARTMENTS table has 3 rows and 2 columns:
| dg id | dg name |
|---|---|
| 200 | DG Communications |
| 400 | DG Innovation and Research |
| 600 | DG Legal Service |
Cartesian Product of these two tables, will produce a Result Table with 5x3=15 Rows, and 4+2=6 Columns as seen below:
| staff id | name | dg id | program no | dg id | dg name |
|---|---|---|---|---|---|
| 802 | YILDIZ | 400 | 10 | 200 | DG Communications |
| 802 | YILDIZ | 400 | 10 | 400 | DG Innovation and Research |
| 802 | YILDIZ | 400 | 10 | 600 | DG Legal Service |
| 804 | HEYNEN | 400 | 20 | 200 | DG Communications |
| 804 | HEYNEN | 400 | 20 | 400 | DG Innovation and Research |
| 804 | HEYNEN | 400 | 20 | 600 | DG Legal Service |
| 806 | KANUITH | 400 | 30 | 200 | DG Communications |
| 806 | KANUITH | 400 | 30 | 400 | DG Innovation and Research |
| 806 | KANUITH | 400 | 30 | 600 | DG Legal Service |
| 808 | ZABOROWSKI | 400 | 40 | 200 | DG Communications |
| 808 | ZABOROWSKI | 400 | 40 | 400 | DG Innovation and Research |
| 808 | ZABOROWSKI | 400 | 40 | 600 | DG Legal Service |
| 1020 | OTTOVA | 400 | 60 | 200 | DG Communications |
| 1020 | OTTOVA | 400 | 60 | 400 | DG Innovation and Research |
| 1020 | OTTOVA | 400 | 60 | 600 | DG Legal Service |
We have already used the ASSIGNMENT (=) Operator in the previous examples as seen below:
If we are interested in STAFF information, but we also want to see the Department Name which is NOT IN THE STAFF TABLE, then a JOIN Operation can be carried out using the STAFF and the DEPARTMENTS tables.
The dg_id column is the common column having the same domain in both tables, and it will be used for the JOIN Operation.
This expression is read as:
In Relational Algebra, the logic behind the JOIN Operation can be depicted as follows:
A PRODUCT Operation on the STAFF and DEPARTMENTS tables is performed first.
The Resulting Table T1 will have 15 Rows and 6 Columns.
| staff id | name | dg id | program no | dg id | dg name |
|---|---|---|---|---|---|
| 802 | YILDIZ | 400 | 10 | 200 | DG Communications |
| 802 | YILDIZ | 400 | 10 | 400 | DG Innovation and Research |
| 802 | YILDIZ | 400 | 10 | 600 | DG Legal Service |
| 804 | HEYNEN | 400 | 20 | 200 | DG Communications |
| 804 | HEYNEN | 400 | 20 | 400 | DG Innovation and Research |
| 804 | HEYNEN | 400 | 20 | 600 | DG Legal Service |
| 806 | KANUITH | 400 | 30 | 200 | DG Communications |
| 806 | KANUITH | 400 | 30 | 400 | DG Innovation and Research |
| 806 | KANUITH | 400 | 30 | 600 | DG Legal Service |
| 808 | ZABOROWSKI | 400 | 40 | 200 | DG Communications |
| 808 | ZABOROWSKI | 400 | 40 | 400 | DG Innovation and Research |
| 808 | ZABOROWSKI | 400 | 40 | 600 | DG Legal Service |
| 1020 | OTTOVA | 400 | 60 | 200 | DG Communications |
| 1020 | OTTOVA | 400 | 60 | 400 | DG Innovation and Research |
| 1020 | OTTOVA | 400 | 60 | 600 | DG Legal Service |
A SELECTION Operation on the Resulting Table T1 of Step 1 is performed next, selecting only those rows where dg_id = dg_id in T1.
Those rows in T1 where dg_id = dg_id are highlighted below.
| staff id | name | dg id | program no | dg id | dg name |
|---|---|---|---|---|---|
| 802 | YILDIZ | 400 | 10 | 200 | DG Communications |
| 802 | YILDIZ | 400 | 10 | 400 | DG Innovation and Research |
| 802 | YILDIZ | 400 | 10 | 600 | DG Legal Service |
| 804 | HEYNEN | 400 | 20 | 200 | DG Communications |
| 804 | HEYNEN | 400 | 20 | 400 | DG Innovation and Research |
| 804 | HEYNEN | 400 | 20 | 600 | DG Legal Service |
| 806 | KANUITH | 400 | 30 | 200 | DG Communications |
| 806 | KANUITH | 400 | 30 | 400 | DG Innovation and Research |
| 806 | KANUITH | 400 | 30 | 600 | DG Legal Service |
| 808 | ZABOROWSKI | 400 | 40 | 200 | DG Communications |
| 808 | ZABOROWSKI | 400 | 40 | 400 | DG Innovation and Research |
| 808 | ZABOROWSKI | 400 | 40 | 600 | DG Legal Service |
| 1020 | OTTOVA | 400 | 60 | 200 | DG Communications |
| 1020 | OTTOVA | 400 | 60 | 400 | DG Innovation and Research |
| 1020 | OTTOVA | 400 | 60 | 600 | DG Legal Service |
The Resulting Table T2 of this SELECTION Operation on table T1, T2 = SEL(T1: dg_id=dg_id) can be seen below:
| staff id | name | dg id | program no | dg id | dg name |
|---|---|---|---|---|---|
| 802 | YILDIZ | 400 | 10 | 400 | DG Innovation and Research |
| 804 | HEYNEN | 400 | 20 | 400 | DG Innovation and Research |
| 806 | KANUITH | 400 | 30 | 400 | DG Innovation and Research |
| 808 | ZABOROWSKI | 400 | 40 | 400 | DG Innovation and Research |
| 1020 | OTTOVA | 400 | 60 | 400 | DG Innovation and Research |
A PROJECTION Operation is performed next on Table T2, eliminating the DUPLICATE dg_id Columns in T2.
T3 = T2(staff_id, name, program_no, dg_id, dg_name )
Table T3 is the Result Table of the JOIN Operation.
| staff id | name | program no | dg id | dg name |
|---|---|---|---|---|
| 802 | YILDIZ | 10 | 400 | DG Innovation and Research |
| 804 | HEYNEN | 20 | 400 | DG Innovation and Research |
| 806 | KANUITH | 30 | 400 | DG Innovation and Research |
| 808 | ZABOROWSKI | 40 | 400 | DG Innovation and Research |
| 1020 | OTTOVA | 60 | 400 | DG Innovation and Research |
The Resulting Table TABLE_H of this JOIN Operation on STAFF and DEPARTMENTS tables, which is explained in detail in Step 1, Step 2, and Step 3 above can now be seen below.
| staff id | name | program no | dg id | dg name |
|---|---|---|---|---|
| 802 | YILDIZ | 10 | 400 | DG Innovation and Research |
| 804 | HEYNEN | 20 | 400 | DG Innovation and Research |
| 806 | KANUITH | 30 | 400 | DG Innovation and Research |
| 808 | ZABOROWSKI | 40 | 400 | DG Innovation and Research |
| 1020 | OTTOVA | 60 | 400 | DG Innovation and Research |
DIVISION Operation in Relational Algebra is similar to the DIVISION Operation in Mathematics.
Problem
We want to find out those Projects that take place in each and every Program.
| program no | project no | number of projects |
|---|---|---|
| 10 | 100 | 2 |
| 10 | 200 | 4 |
| 20 | 100 | 1 |
| 20 | 300 | 1 |
| 30 | 100 | 2 |
| 30 | 200 | 2 |
| 30 | 300 | 4 |
| 30 | 400 | 3 |
| 40 | 100 | 2 |
| 60 | 100 | 1 |
| project no | project type | description | main sponsor | cost (million Euros) |
|---|---|---|---|---|
| 100 | ATOMS | Nano Technology | Futuristic | 2.37 |
| 200 | BITS | Information Technology | Guru | 6.19 |
| 300 | GENES | Bio Technology | Longevity | 4.48 |
| 400 | NEURONS | Neuro Science | Cyberlabs | 1.49 |
Answer
To be able to find the Answer to the Question "Which Projects take place in each and every Program?" we perform the DIVISION Operation.
TABLE_I = PROGRAM_PROJECTS DIVISION PROJECTS
TABLE_I = PROGRAM_PROJECTS / PROJECTS
Project no 100, whose project type is 'ATOMS' and described as 'Nano Technology', takes place in each and every Program of this Research Institution.
Hence, the Result Table TABLE_I of this DIVISION Operation will only hold one row with project_no=100.
| project no |
|---|
| 100 |
In Relational Algebra, DIVISION identifies rows in one table that have certain relationship to all rows in another table.
By using the Division Operation, a Relationship creates a New Entity from an Existing Entity.
Another Solution for Problem 1
Problem 1
Referring to the Sample Database Tables, find out the "name of staff" who was responsible of the Projects in Belgium, Last Year.
Solution for Problem 1
Step 1
Use the SELECTION Operation on the PROGRAMS_LAST_YEAR table to find the program where the country is Belgium.
TABLE_A = SEL(PROGRAMS_LAST_YEAR: country='Belgium')
| program no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 20 | Brussels | Belgium |
| 30 | Luxembourg | Luxembourg |
The program that took place last year in Belgium is program_no=20.
Result Table TABLE_A of this SELECTION Operation is seen below.
| program no | location | country |
|---|---|---|
| 20 | Brussels | Belgium |
Step 2
Use the JOIN Operation on the STAFF table and the Result Table TABLE_A from Step 1 to find the staff who is responsible of the chosen program.
| staff id | name | dg id | program_no |
|---|---|---|---|
| 802 | YILDIZ | 400 | 10 |
| 804 | HEYNEN | 400 | 20 |
| 806 | KANUITH | 400 | 30 |
| 808 | ZABOROWSKI | 400 | 40 |
| 1020 | OTTOVA | 400 | 60 |
We can see above the row in the STAFF table where program_no=20.
This gives us the Resulting Table TABLE_B.
| staff id | name | dg id | program_no |
|---|---|---|---|
| 804 | HEYNEN | 400 | 20 |
Step 3
Now that we have the staff responsible for the program in Belgium last year, as seen in TABLE_B of Step 2, we can use the PROJECTION Operation on TABLE_B to find his/her name.
| name |
|---|
| HEYNEN |
The answer is HEYNEN.
This resumes the Solution of Problem 1.
Another Solution for Problem 1
An alternative solution to this problem is seen below.
Step 1
Use the JOIN Operation on PROGRAMS_LAST_YEAR and STAFF to build up the Result Table TABLE_1.
TABLE_1= JOIN(PROGRAMS_LAST_YEAR,STAFF: program_no=program_no)
| program no | location | country | staff id | name | dg id |
|---|---|---|---|---|---|
| 10 | Istanbul | Turkey | 802 | YILDIZ | 400 |
| 20 | Brussels | Belgium | 804 | HEYNEN | 400 |
| 30 | Luxembourg | Luxembourg | 806 | KANUITH | 400 |
Step 2
Use the SELECTION Operation on TABLE_1 to build up the Result Table TABLE_2.
TABLE_2=SEL(TABLE_1: country='Belgium')
| program no | location | country | staff id | name | dg id |
|---|---|---|---|---|---|
| 20 | Brussels | Belgium | 804 | HEYNEN | 400 |
Step 3
Use the PROJECTION Operation on TABLE_2 to build up the Result Table TABLE_3.
TABLE_3=TABLE_2(name)
| name |
|---|
| HEYNEN |
This resumes the alternative solution for Problem 1.
Problem 2
Referring to the Sample Database Tables, find out the Descriptions and the Main Sponsors for the Projects in Belgium.
Solution for Problem 2
Step 1
Use the UNION Operation to put all the Programs together, since we do not know whether the Programs in Belgium took place Last Year or they are taking place This Year.
Resulting Table T1 = PROGRAMS_LAST_YEAR UNION PROGRAMS_THIS_YEAR
| program_no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 20 | Brussels | Belgium |
| 30 | Luxembourg | Luxembourg |
| 40 | Warsaw | Poland |
| 60 | Prague | Czech Republic |
Step 2
Use the SELECTION Operation on the Resulting Table T1 from Step 1, to find the Programs in Belgium.
Resulting Table T2 = SEL(T1: country='Belgium')
| program_no | location | country |
|---|---|---|
| 20 | Brussels | Belgium |
Step 3
Use the JOIN Operation on the Resulting Table T2 from Step 2, and table PROGRAM_PROJECTS to find out all the Projects in this Program.
Resulting Table T3 = JOIN(T2,PROGRAM_PROJECTS: program_no=program_no)
| program no | project no | number of projects |
|---|---|---|
| 10 | 100 | 2 |
| 10 | 200 | 4 |
| 20 | 100 | 1 |
| 20 | 300 | 1 |
| 30 | 100 | 2 |
| 30 | 200 | 2 |
| 30 | 300 | 4 |
| 30 | 400 | 3 |
| 40 | 100 | 2 |
| 60 | 100 | 1 |
| program no | location | country | project no | number of projects |
|---|---|---|---|---|
| 20 | Brussels | Belgium | 100 | 1 |
| 20 | Brussels | Belgium | 300 | 1 |
Step 4
Use the JOIN Operation on the Resulting Table T3 from Step 3, and table PROJECTS to find out all the information about the selected Projects.
Resulting Table T4 = JOIN(T3,PROJECTS: project_no=project_no)
| project no | project type | description | main sponsor | cost (million Euros) |
|---|---|---|---|---|
| 100 | ATOMS | Nano Technology | Futuristic | 2.37 |
| 200 | BITS | Information Technology | Guru | 6.19 |
| 300 | GENES | Bio Technology | Longevity | 4.48 |
| 400 | NEURONS | Neuro Science | Cyberlabs | 1.49 |
| program no | location | country | project no | number of projects | project type | description | main sponsor | cost |
|---|---|---|---|---|---|---|---|---|
| 20 | Brussels | Belgium | 100 | 1 | ATOMS | Nano Technology | Futuristic | 2.37 |
| 20 | Brussels | Belgium | 300 | 1 | GENES | Bio Technology | Longevity | 4.48 |
Step 5
Use the PROJECTION Operation on the Resulting Table T4 from Step 4, to retrieve the Descriptions and Names of the Main Sponsors of the Projects in Belgium.
Resulting Table T5 = T4 (description, main_sponsor)
| description | main sponsor |
|---|---|
| Nano Technology | Futuristic |
| Bio Technology | Longevity |
This resumes the Solution for Problem 2.
Relational Calculus is a non-procedural language.
The programmer specifies the data requirement, and the system generates the operations needed to produce a table with the required data.
Relational Calculus uses the general syntax:
Result = (Column List): Expression
Solution for Problem 1 in Relational Calculus
Solution for Problem 1 in Relational Algebra
Solution for Problem 2 in Relational Calculus
Solution for Problem 2 in Relational Algebra
Solution for Problem 3 in Relational Calculus
Solution for Problem 3 in Relational Algebra
Problem 1
Referring to the Sample Database Tables, find those programs that contain project number 400.
Solution for Problem 1 in Relational Calculus
In Relational Calculus, the User/Programmer writes down the expressions necessary to solve this problem as follows:
(r.program_no) :
r in PROGRAM_PROJECTS
AND r.project_no = 400
In this expression, r is known as a row variable.
The expression is read as;
program_no in row r, where r is a row in the PROGRAM_PROJECTS table and project_no in row r is 400
Each row in PROGRAM_PROJECTS is examined using the condition to the right of the column.
| program no | project no | number of_projects |
|---|---|---|
| 10 | 100 | 2 |
| 10 | 200 | 4 |
| 20 | 100 | 1 |
| 20 | 300 | 1 |
| 30 | 100 | 2 |
| 30 | 200 | 2 |
| 30 | 300 | 4 |
| 30 | 400 | 3 |
| 40 | 100 | 2 |
| 60 | 100 | 1 |
The Resulting Table T contains the program_no column where its value is 30.
| program no |
|---|
| 30 |
This solution is in Relational Calculus.
In Relational Calculus, the system generated the required operations and produced the Resulting Table T with the required data, using the expressions given by the User/Programmer.
Solution for Problem 1 in Relational Algebra
Solution for the same problem in Relational Algebra would look like the following.
Step 1
Use the SELECTION Operation on the PROGRAM_PROJECTS table to select the rows where project_no=400.
Resulting Table T1 = SEL(PROGRAM_PROJECTS : project_no = 400)
| program no | project no | number of projects |
|---|---|---|
| 10 | 100 | 2 |
| 10 | 200 | 4 |
| 20 | 100 | 1 |
| 20 | 300 | 1 |
| 30 | 100 | 2 |
| 30 | 200 | 2 |
| 30 | 300 | 4 |
| 30 | 400 | 3 |
| 40 | 100 | 2 |
| 60 | 100 | 1 |
| program no | project no | number of projects |
|---|---|---|
| 30 | 400 | 3 |
Step 2
Use the PROJECTION Operation on the Resulting Table T1 from Step1, to select the required column program_no.
Resulting Table T2 = T1(program_no)
| program no |
|---|
| 30 |
This resumes the Solution for Problem 1, using Relational Algebra.
Problem 2
Referring to the Sample Database Tables, find the"staff_id" and "name" of staff members who work in department DG Innovation and Research.
Solution for Problem 2 in Relational Calculus
In Relational Calculus, the User/Programmer writes down the expressions necessary to solve this problem as follows:
(r.staff_id, r.name) :
r in STAFF
AND s in DEPARTMENTS
AND r.dg_id= s.dg_id
AND s.dg_name = 'DG Innovation and Research'
The Resulting Table T is as follows:
| staff id | name |
|---|---|
| 802 | YILDIZ |
| 804 | HEYNEN |
| 806 | KANUITH |
| 808 | ZABOROWSKI |
| 1020 | OTTOVA |
This solution is in Relational Calculus.
In Relational Calculus, the system generated the required operations and produced the Resulting Table T, using the expressions given by the User/Programmer.
Solution for Problem 2 in Relational Algebra
Solution for the same problem in Relational Algebra would look like the following.
Step 1
Use the SELECTION Operation on DEPARTMENTS Table to find the rows where Department Name (dg_name) is 'DG Innovation and Research'.
Resulting Table T1 = SEL(DEPARTMENTS : dg_name = 'DG Innovation and Research')
| dg id | dg name | 200 | DG Communications |
|---|---|
| 400 | DG Innovation and Research |
| 600 | DG Legal Service |
| dg id | dg name |
|---|---|
| 400 | DG Innovation and Research |
Step 2
Use the JOIN Operation on the Resulting Table T1 from Step 1, and the STAFF Table, to find those rows where their Department IDs(dg_id) are equal.
Resulting Table T2 = JOIN(T1,STAFF : dg_id = dg_id)
| staff id | name | dg id | program no |
|---|---|---|---|
| 802 | YILDIZ | 400 | 10 |
| 804 | HEYNEN | 400 | 20 |
| 806 | KANUITH | 400 | 30 |
| 808 | ZABOROWSKI | 400 | 40 |
| 1020 | OTTOVA | 400 | 60 |
| staff id | name | dg id | program no | dg name |
|---|---|---|---|---|
| 802 | YILDIZ | 400 | 10 | DG Innovation and Research |
| 804 | HEYNEN | 400 | 20 | DG Innovation and Research |
| 806 | KANUITH | 400 | 30 | DG Innovation and Research |
| 808 | ZABOROWSKI | 400 | 40 | DG Innovation and Research |
| 1020 | OTTOVA | 400 | 60 | DG Innovation and Research |
Step 3
Use the PROJECTION Operation on the Resulting Table T2 from Step 2 to find the values of columns staff_id and name.
Resulting Table T3 = T2(staff_id, name)
| staff id | name |
|---|---|
| 802 | YILDIZ |
| 804 | HEYNEN |
| 806 | KANUITH |
| 808 | ZABOROWSKI |
| 1020 | OTTOVA |
This resumes the Solution for Problem 2, using Relational Algebra.
Problem 3
Referring to the Sample Database Tables, find the staff name, department name, and location for Projects taking place This Year for the Staff responsible for Program Number 10.
Solution for Problem 3 in Relational Calculus
In Relational Calculus, the User/Programmer writes down the expressions necessary to solve this problem as follows:
(e.name, d.dg_name, p.location) :
e in STAFF
AND d in DEPARTMENTS
AND p in PROGRAMS_THIS_YEAR
AND e.dg_id = d.dg_id
AND e.program_no = p.program_no
AND p.program_no = 10
The Resulting Table T is seen below:
| name | dg name | location |
|---|---|---|
| YILDIZ | DG Innovation and Research | Istanbul |
This solution is in Relational Calculus.
In Relational Calculus, the system generated the required operations and produced the Resulting Table T with the required data, using the expressions given by the User/Programmer.
Solution for Problem 3 in Relational Algebra
Solution for the same problem in Relational Algebra would look like the following.
Step 1
Use the SELECTION Operation on Table PROGRAMS_THIS_YEAR to find those rows, where program_no=10.
Resulting Table T1 = SEL(PROGRAMS_THIS_YEAR : program_no = 10)
| program no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
| 30 | Luxembourg | Luxembourg |
| 40 | Warsaw | Poland |
| 60 | Prague | Czech Republic |
| program no | location | country |
|---|---|---|
| 10 | Istanbul | Turkey |
Step 2
Use the JOIN Operation on the Resulting Table T1 from Step 1, and the STAFF table on the common values of the column program_no.
Resulting Table T2 = JOIN(T1,STAFF : program_no=program_no)
| staff id | name | dg id | program no |
|---|---|---|---|
| 802 | YILDIZ | 400 | 10 |
| 804 | HEYNEN | 400 | 20 |
| 806 | KANUITH | 400 | 30 |
| 808 | ZABOROWSKI | 400 | 40 |
| 1020 | OTTOVA | 400 | 60 |
| staff id | name | dg id | program no | location | country |
|---|---|---|---|---|---|
| 802 | YILDIZ | 400 | 10 | Istanbul | Turkey |
Step 3
Use the JOIN Operation on the Resulting Table T2 from Step 2, and the DEPARTMENTS Table on the common values of the column dg_id.
Resulting Table T3 = JOIN(T2,DEPARTMENTS : dg_id = dg_id)
| dg id | dg name |
|---|---|
| 200 | DG Communications |
| 400 | DG Innovation and Research |
| 600 | DG Legal Service |
| staff id | name | dg id | program no | location | country | dg name |
|---|---|---|---|---|---|---|
| 802 | YILDIZ | 400 | 10 | Istanbul | Turkey | DG Innovation and Research |
Step 4
Use the PROJECTION Operation on the Resulting Table T3 from Step 3, to select the columns name, dg_name and location only.
Resulting Table T4 = T3(name, dg_name, location)
| name | dg name | location |
|---|---|---|
| YILDIZ | DG Innovation and Research | Istanbul |
This resumes the Solution for Problem 3, using Relational Algebra.